力と運動

次の問いに答えなさい。 図のようにひもの先におもりがくっついている。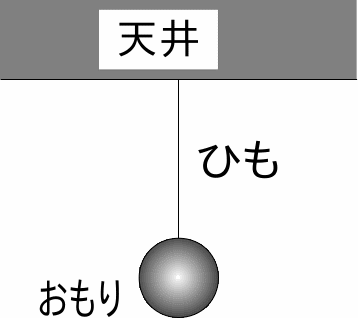
おもりがひもを引く力とつり合っている力を答えなさい。 おもりがひもを引く力と作用反作用の関係にある力を答えなさい。 おもりにかかる重力とつり合っている力を答えなさい。 おもりにかかる重力と作用反作用の関係にある力を答えなさい。 図のように床に物体が置いてある。
床が物体を押す力とつりあっているのは何という力ですか。 床が物体を押す力と作用、反作用の関係にあるのは何という力ですか。 次の文章を読んで下の問に答えなさい。 「8:00にA町をでて50㎞離れたB町まで行った。郊外の道路を走るときにメーターを見たら時速55㎞で、街の中を走るときにメーターを見ると時速35㎞だった。結局9:15にB町についた。」 A町からB町へ行くときの平均の速さは時速何kmか求めなさい。 下線部のような速さを何というか。 グラフは縦軸に速さ、横軸に時間をとったものである。これを見て次の問に答えなさい。 このグラフは等速直線運動、斜面の運動のどちらですか。 ０秒から４秒までの平均の速さを求めなさい。 ０秒から３秒後までに進んだ距離を求めなさい。

つり合う２力とは、１つの物体に対してはたらく２力のことなので力を受けている物体を考える。 「AがBを引く力」では力を受けているのはBである。 つり合いを考えるときは他にBに対してどんな力が加わっているのかを探す。 Bが静止していて、Bに対して加わる力が「AがBを引く力」と「CがBを引く力」だけなら、この２力はつりあっている。
作用反作用の関係の２力は、２つの物体の間で相互に及ぼしあう力のことなので、力を出している物体と、受けている物体の２つを考える。 「XがYを引く力」にはXとYという２つの物体が関係している。 つまり作用反作用の関係にある力はXとYを入れ替えて「YがXを引く力」である。
①
おもりがひもを引く力とは「ひも」に対してはたらく力である。 他に「ひも」にたいして働いているのは「天井がひもを引く力」である。
②
「おもりがひもを引く力」には「おもり」と「ひも」の２つの物体が関係している。 よって「ひもがおもりを引く力」となる。
③
「おもりにかかる重力」とはおもりに対してはたらく力なので、つり合っているのは「ひもがおもりを引く力」である。
④
重力は地球が出している力なので「おもりにかかる重力」をいいかえると「地球がおもりを引く力」となる。 よって作用反作用の関係にあるのは「おもりが地球を引く力」である。
①
「床が物体を押す力」は物体に対してはたらく力である。 ほかに物体に対して働いている力は重力である。
②
「床が物体を押す力」は床と物体の間の力なので「物体が床を押す力」が作用反作用の関係にある。 平均の速さとは　移動した距離をかかった時間で割ると出る。途中の速さが変化しても関係ない。 瞬間の速さとは極めて短い時間で平均の速さを出したものと考えることができる。
(1)
移動距離は50km、　8時に出て9時15分についたのでかかった時間は１時間15分、これを時間で表すと 7560 よって平均の速さは50÷7560 =40
(2)
瞬間の速さの例は車のスピードメーターに表示される速さである。 よく使われるグラフには縦軸に速さをとる場合と、縦軸に距離を取る場合がある。 横軸はどちらも時間である。 縦軸に速さを取る場合、等速直線運動はずっと同じ速度なので横軸に平行なグラフ、斜面の運動は一定の割合で速さが増すグラフになる。
縦軸に距離を取る場合、等速直線運動は一定の割合で距離が増していくので右上がりの直線、斜面の運動は時間の２乗に比例して距離が増す放物線になる。
縦軸が速さで、右上がりの直線なので、斜面の運動である。

縦軸が速さの場合、進んだ距離はグラフの下の部分の面積になる。
0から4秒の場合、図の三角形の面積が距離

よって進んだ距離は8m, かかった時間は4秒なので、平均の速さは8÷4=2 0から3秒までに進んだ距離は図の三角形の面積

よって4.5m